Markus Bibinger from the University of Marburg, Nikolaus Hautsch from the University of Vienna, Peter Malec from the University of Cambridge and Markus Reiss from Humboldt University Berlin published a paper using LOBSTER data. It is titled Estimating the Spot Covariation of Asset Prices — Statistical Theory and Empirical Evidence and is forthcoming in the Journal of Business and Economic Statistics.
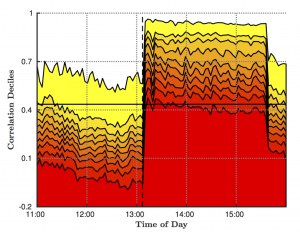
Abstract: We propose a new estimator for the spot covariance matrix of a multi-dimensional continuous semi-martingale log asset price process which is subject to noise and non-synchronous observations. The estimator is constructed based on a local average of block-wise parametric spectral covariance estimates. The latter originate from a local method of moments (LMM) which recently has been introduced by Bibinger et al (2014). We prove consistency and a point-wise stable central limit theorem for the proposed spot covariance estimator in a very general setup with stochastic volatility, leverage effects and general noise distributions. Moreover, we extend the LMM estimator to be robust against autocorrelated noise and propose a method to adaptively infer the autocorrelations from the data. Based on simulations we provide empirical guidance on the effective implementation of the estimator and apply it to high-frequency data of a cross-section of Nasdaq blue chip stocks. Employing the estimator to estimate spot covariances, correlations and volatilities in normal but also unusual periods yields novel insights into intraday covariance and correlation dynamics. We show that intraday (co-)variations (i) follow underlying periodicity patterns, (ii) reveal substantial intraday variability associated with (co-)variation risk, and (iii) can increase strongly and nearly instantaneously if new information arrives.
A working paper version is found here.